技术笔记04-基于间接飞行时间的连续波技术（CW-iToF）中双频调制是什么？

根据公式 d_max= c/2f，可以知道频率越低，测量距离的最大值越大，这会伴随着相对精度和绝对精度降低或较大抖动的问题。相反，频率越高，精度越高，但增加频率会导致测量距离减少。解决连续波(CW-iToF)过周期现象的一种方法是双频测量，即对同一测量对象使用两个不同的频率，并从两次测量的结果中确定真实距离。目前，我们的CW-iToF相机使用高频120MHz来提高测量精度，并使用低频20MHz来推导当前周期数以确定最终的真实距离。在本文中，让我们理解一下如何计算双频的真实距离。

计算双频的最大探测距离

假设频率为f_A的相位是φ_A，频率为f_B的相位是φ_B，光速为c，频率f_A的最大探测距离d_A=c/2 f_A，频率f_B的最大探测距离d_B=c/2f_B，最大距离由双频最大公约数f_E决定，计算如下：

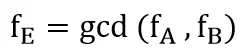
将f_A：f_B化简成互为质数的比值M_A：M_B，

假设φ_A模糊次数为n_A（0 ≤ n_A ≤ M_A-1），φ_B模糊次数为n_B（0 ≤ n_B ≤ M_B-1），
将相位角φ_A和φ_B转换到[0，1]范围内：

真实的距离可以计算为：d_true = d_A x（n_A + P_A）= d_B x（n_B + P_B），需求解n_A和n_B为何值时。
当|d_A x（n_A + P_A）-d_B x（n_B + P_B）|取得最小值，可以求出n_A与n_B。又因为

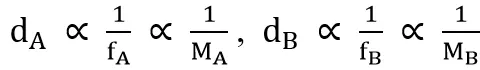
因此，可以将n_A与n_B求解转为求下式的最小值：

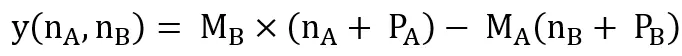
因此，计算真实距离的公式d_true：

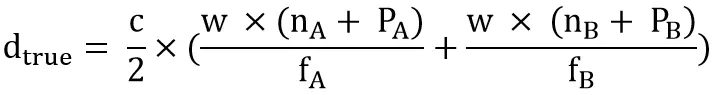
应用举例
假设两个测量频率分别为f_A = 30MHZ，f_B = 40MHZ，频率f_A的测量距离为4.0m，频率f_B的测量距离为1.5m，双频下的测量距离求解如下：
频率f_A的最大测量距离为d_A：

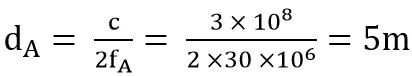
频率f_B的最大测量距离为d_B：

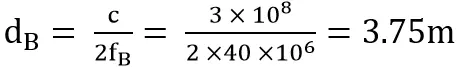
f_A与f_B的最大公约数f_E = gcd（f_A，f_B）=10MHZ，

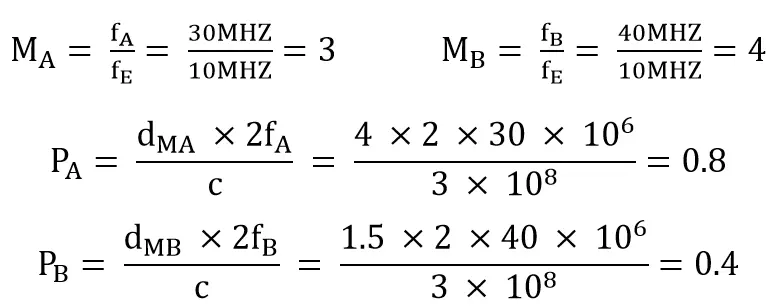
经计算，当n_A = 1，n_B = 2，y(n_A, n_B) = M_B ×(n_A + P_A) – M_A ×(n_B + P_B)最小。
最终测得真实距离为：d_true = 5×(1 + 0.8 ) = 9m。

不同频率组合下的理论最大测量距离和错误率

下表显示了不同高频和低频组合理论的最大值：

高频（MHZ）	低频（MHZ）	理论最大距离
100	15	30
100	45	30
100	65	30
100	10	15
100	30	15
100	70	15
100	20	7.5
100	60	7.5
100	80	7.5
100	25	6
100	50	3

	错误率/%	错误率/%	错误率/%
距离/m	100MHZ&90MHZ	100MHZ&80MHZ	100MHZ&60MHZ
0.5	0	0	0
1.0	0	0	0
1.5	0	0	0
2.0	0.4	0	0
2.5	0.8	0	0
3.0	4.4	0	0
3.5	12.7	0.4	0.1
4.0	22.7	1.3	0.9
4.5	32.9	5	1.6
5.0	40.8	10.4	8.3
5.5	48.7	16	12.2
6.0	34.8	21.6	18.9
6.5	28	31.3	30
7.0	32.6	39	34.4